mirror of
https://github.com/ROCm/jax.git
synced 2025-04-15 19:36:06 +00:00
populate readme with ill content
This commit is contained in:
parent
ee1728c2af
commit
948a8db0ad
633
README.md
633
README.md
@ -1,5 +1,630 @@
|
|||||||
JAX is a research project that grew out of [Autograd](https://github.com/hips/autograd).
|
# JAX: Autograd and XLA
|
||||||
Here's a [two-page abstract](https://www.sysml.cc/doc/146.pdf) about an early version.
|
|
||||||
Watch this space for updates!
|
|
||||||
|
|
||||||
This is not an official Google product.
|

|
||||||
|
|
||||||
|
[JAX](http://go/jax) is [Autograd](https://github.com/hips/autograd) and
|
||||||
|
[XLA](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/compiler/xla/g3doc/overview.md),
|
||||||
|
brought together for high-performance machine learning research.
|
||||||
|
|
||||||
|
With its updated version of [Autograd](https://github.com/hips/autograd), JAX
|
||||||
|
can automatically differentiate native Python and NumPy code. It can
|
||||||
|
differentiate through a large subset of Python’s features, including loops,
|
||||||
|
ifs, recursion, and closures, and it can even take derivatives of derivatives
|
||||||
|
of derivatives. It supports reverse-mode differentiation (a.k.a.
|
||||||
|
backpropagation) as well as forward-mode differentiation, and the two can be
|
||||||
|
composed arbitrarily to any order.
|
||||||
|
|
||||||
|
What’s new is that JAX uses
|
||||||
|
[XLA](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/compiler/xla/g3doc/overview.md)
|
||||||
|
to compile and run your NumPy code on accelerators, like GPUs and TPUs.
|
||||||
|
Compilation happens under the hood by default, with library calls getting
|
||||||
|
just-in-time compiled and executed. But JAX even lets you just-in-time compile
|
||||||
|
your own Python functions into XLA-optimized kernels using a one-function API.
|
||||||
|
Compilation and automatic differentiation can be composed arbitrarily, so you
|
||||||
|
can express sophisticated algorithms and get maximal performance without having
|
||||||
|
to leave Python.
|
||||||
|
|
||||||
|
This is a research project, not an official Google product. Expect bugs and
|
||||||
|
sharp edges. Please help by trying it out, [reporting
|
||||||
|
bugs](https://github.com/google/jax/issues), and letting us know what you
|
||||||
|
think!
|
||||||
|
|
||||||
|
```python
|
||||||
|
import jax.numpy as np
|
||||||
|
from jax import grad, jit, vmap
|
||||||
|
from functools import partial
|
||||||
|
|
||||||
|
def predict(params, inputs):
|
||||||
|
for W, b in params:
|
||||||
|
outputs = np.dot(inputs, W) + b
|
||||||
|
inputs = np.tanh(outputs)
|
||||||
|
return outputs
|
||||||
|
|
||||||
|
def logprob_fun(params, inputs, targets):
|
||||||
|
preds = predict(params, inputs)
|
||||||
|
return np.sum((preds - targets)**2)
|
||||||
|
|
||||||
|
grad_fun = jit(grad(logprob_fun)) # compiled gradient evaluation function
|
||||||
|
perex_grads = jit(lambda params, inputs, targets: # fast per-example gradients
|
||||||
|
vmap(partial(grad_fun, params), inputs, targets))
|
||||||
|
```
|
||||||
|
|
||||||
|
JAX started as a research project by [Matt Johnson](https://github.com/mattjj),
|
||||||
|
[Roy Frostig](https://github.com/froystig), [Dougal
|
||||||
|
Maclaurin](https://github.com/dougalm), and [Chris
|
||||||
|
Leary](https://github.com/learyg), and is now developed [in the
|
||||||
|
open](https://github.com/google/jax) by a growing number of
|
||||||
|
[contributors](#contributors).
|
||||||
|
|
||||||
|
## Quickstart: Colab in the Cloud
|
||||||
|
Jump right in using [a notebook in your
|
||||||
|
browser](https://colab.research.google.com/github/google/jax/blob/master/notebooks/quickstart.ipynb)
|
||||||
|
connected to a Google Cloud GPU.
|
||||||
|
|
||||||
|
## Installation
|
||||||
|
JAX is written in pure Python, but it depends on XLA, which needs to be
|
||||||
|
compiled and installed as the `jaxlib` package. Use the following instructions
|
||||||
|
to [build XLA from source](#building-jax-from-source) or [install a binary
|
||||||
|
package with pip](#pip-installation).
|
||||||
|
|
||||||
|
### Building JAX from source
|
||||||
|
First, obtain the JAX source code:
|
||||||
|
|
||||||
|
```bash
|
||||||
|
git clone https://github.com/google/jax
|
||||||
|
cd jax
|
||||||
|
```
|
||||||
|
|
||||||
|
To build XLA with CUDA support, you can run
|
||||||
|
|
||||||
|
```bash
|
||||||
|
python build/build.py --enable_cuda
|
||||||
|
pip install -e build # install jaxlib
|
||||||
|
pip install -e . # install jax
|
||||||
|
```
|
||||||
|
|
||||||
|
See `python build/build.py --help` for configuration options, including ways to
|
||||||
|
specify the paths to CUDA and CUDNN, which you must have installed. The build
|
||||||
|
also depends on NumPy, and a compiler toolchain corresponding to that of
|
||||||
|
Ubuntu 16.04 or newer.
|
||||||
|
|
||||||
|
To build XLA without CUDA GPU support (CPU only), just run
|
||||||
|
|
||||||
|
```bash
|
||||||
|
python build/build.py
|
||||||
|
pip install -e build # install jaxlib
|
||||||
|
pip install -e . # install jax
|
||||||
|
```
|
||||||
|
|
||||||
|
To update to the latest version from GitHub, just run `git pull` from the JAX
|
||||||
|
repository root, and rebuild by running `build.py` if necessary. You only have
|
||||||
|
to reinstall if new files are added because `pip install -e` sets up symbolic
|
||||||
|
links from site-packages into the repository.
|
||||||
|
|
||||||
|
### pip installation
|
||||||
|
|
||||||
|
Installing XLA with prebuilt binaries via `pip` is still experimental,
|
||||||
|
especially with GPU support. Let us know on [the issue
|
||||||
|
tracker](https://github.com/google/jax/issues) if you run into any errors.
|
||||||
|
|
||||||
|
To install a CPU-only version, which might be useful for doing local
|
||||||
|
development on a laptop, you can run
|
||||||
|
|
||||||
|
```bash
|
||||||
|
pip install jax jaxlib
|
||||||
|
```
|
||||||
|
|
||||||
|
If you want to install JAX with both CPU and GPU support, using existing CUDA
|
||||||
|
and CUDNN7 installations on your machine (for example, preinstalled on your
|
||||||
|
cloud VM), you can run
|
||||||
|
|
||||||
|
```bash
|
||||||
|
# install jaxlib
|
||||||
|
PYTHON_VERSION=py2 # alternatives: py2, py3
|
||||||
|
CUDA_VERSION=cuda92 # alternatives: cuda90, cuda92, cuda100
|
||||||
|
PLATFORM=linux_x86_64 # alternatives: linux_x86_64, mac
|
||||||
|
pip install https://storage.googleapis.com/jax-wheels/$CUDA_VERSION/jax-0.1-$PYTHON_VERSION-none-$PLATFORM.whl
|
||||||
|
|
||||||
|
pip install jax # install jax
|
||||||
|
```
|
||||||
|
|
||||||
|
The library package name must correspond to the version of the existing CUDA
|
||||||
|
installation you want to use, with `cuda100` for CUDA 10.0, `cuda92` for CUDA
|
||||||
|
9.2, and `cuda90` for CUDA 9.0. To find your CUDA and CUDNN versions, you can
|
||||||
|
run command like these, depending on your CUDNN install path:
|
||||||
|
|
||||||
|
```bash
|
||||||
|
nvcc --version
|
||||||
|
grep CUDNN_MAJOR -A 2 /usr/local/cuda/include/cudnn.h # might need different path
|
||||||
|
```
|
||||||
|
|
||||||
|
## A brief tour
|
||||||
|
|
||||||
|
```python
|
||||||
|
In [1]: import jax.numpy as np
|
||||||
|
|
||||||
|
In [2]: from jax import random
|
||||||
|
|
||||||
|
In [3]: key = random.PRNGKey(0)
|
||||||
|
|
||||||
|
In [4]: x = random.normal(key, (5000, 5000))
|
||||||
|
|
||||||
|
In [5]: print(np.dot(x, x.T) / 2) # fast!
|
||||||
|
[[ 2.52727051e+03 8.15895557e+00 -8.53276134e-01 ..., # ...
|
||||||
|
|
||||||
|
In [6]: print(np.dot(x, x.T) / 2) # even faster!
|
||||||
|
[[ 2.52727051e+03 8.15895557e+00 -8.53276134e-01 ..., # ...
|
||||||
|
```
|
||||||
|
|
||||||
|
What’s happening behind-the-scenes is that JAX is using XLA to just-in-time
|
||||||
|
(JIT) compile and execute these individual operations on the GPU. First the
|
||||||
|
`random.normal` call is compiled and the array referred to by `x` is generated
|
||||||
|
on the GPU. Next, each function called on `x` (namely `transpose`, `dot`, and
|
||||||
|
`divide`) is JIT-compiled and executed, each keeping its results on the device.
|
||||||
|
It’s only when a value needs to be printed, plotted, saved, or passed into a raw
|
||||||
|
NumPy function that a read-only copy of the value is brought back to the host as
|
||||||
|
an ndarray and cached. The second call to `dot` is even faster because the
|
||||||
|
JIT-compiled code is cached and reused, saving the compilation time.
|
||||||
|
|
||||||
|
The fun really starts when you use `grad` for automatic differentiation and
|
||||||
|
`jit` to compile your own functions end-to-end. Here’s a more complete toy
|
||||||
|
example:
|
||||||
|
|
||||||
|
```python
|
||||||
|
from jax import grad, jit
|
||||||
|
import jax.numpy as np
|
||||||
|
|
||||||
|
def sigmoid(x):
|
||||||
|
return 0.5 * (np.tanh(x / 2.) + 1)
|
||||||
|
|
||||||
|
# Outputs probability of a label being true according to logistic model.
|
||||||
|
def logistic_predictions(weights, inputs):
|
||||||
|
return sigmoid(np.dot(inputs, weights))
|
||||||
|
|
||||||
|
# Training loss is the negative log-likelihood of the training labels.
|
||||||
|
def loss(weights, inputs, targets):
|
||||||
|
preds = logistic_predictions(weights, inputs)
|
||||||
|
label_probs = preds * targets + (1 - preds) * (1 - targets)
|
||||||
|
return -np.sum(np.log(label_probs))
|
||||||
|
|
||||||
|
# Build a toy dataset.
|
||||||
|
inputs = np.array([[0.52, 1.12, 0.77],
|
||||||
|
[0.88, -1.08, 0.15],
|
||||||
|
[0.52, 0.06, -1.30],
|
||||||
|
[0.74, -2.49, 1.39]])
|
||||||
|
targets = np.array([True, True, False, True])
|
||||||
|
|
||||||
|
# Define a compiled function that returns gradients of the training loss
|
||||||
|
training_gradient_fun = jit(grad(loss))
|
||||||
|
|
||||||
|
# Optimize weights using gradient descent.
|
||||||
|
weights = np.array([0.0, 0.0, 0.0])
|
||||||
|
print("Initial loss: {:0.2f}".format(loss(weights, inputs, targets)))
|
||||||
|
for i in range(100):
|
||||||
|
weights -= 0.1 * training_gradient_fun(weights, inputs, targets)
|
||||||
|
|
||||||
|
print("Trained loss: {:0.2f}".format(loss(weights, inputs, targets)))
|
||||||
|
```
|
||||||
|
|
||||||
|
To see more, check out the [quickstart
|
||||||
|
notebook](https://colab.research.google.com/github/google/jax/blob/master/notebooks/quickstart.ipynb),
|
||||||
|
a [simple MNIST classifier
|
||||||
|
example](https://github.com/google/jax/blob/master/examples/mnist_classifier.py)
|
||||||
|
and the rest of the [JAX
|
||||||
|
examples](https://github.com/google/jax/blob/master/examples/).
|
||||||
|
|
||||||
|
## What's supported
|
||||||
|
|
||||||
|
If you’re using JAX just as an accelerator-backed NumPy, without using `grad` or
|
||||||
|
`jit` in your code, then in principle there are no constraints, though some
|
||||||
|
NumPy features haven’t been implemented. Generally using `np.dot(A, B)` is
|
||||||
|
better than `A.dot(B)` because the former gives us more opportunities to run the
|
||||||
|
computation on the device. NumPy also does a lot of work to cast any array-like
|
||||||
|
function arguments to arrays, as in `np.sum([x, y])`, while `jax.numpy`
|
||||||
|
typically requires explicit casting of array arguments, like
|
||||||
|
`np.sum(np.array([x, y]))`.
|
||||||
|
|
||||||
|
For automatic differentiation with `grad`, JAX has the same basic requirements
|
||||||
|
as [Autograd](https://github.com/hips/autograd). Specifically, differentiation
|
||||||
|
works with indexing (`x = A[i, j, :]`) but not indexed assignment (`A[i, j] =
|
||||||
|
x`) or indexed in-place updating (`A[i] += b`). You can use lists, tuples, and
|
||||||
|
dicts freely. Using `np.dot(A, B)` rather than `A.dot(B)` is required for
|
||||||
|
automatic differentiation when `A` is a raw ndarray.
|
||||||
|
|
||||||
|
For compiling your own functions with `jit` there are a few more requirements.
|
||||||
|
Because `jit` aims to specialize Python functions only on shapes and dtypes
|
||||||
|
during tracing, rather than on concrete values, Python control flow that depends
|
||||||
|
on concrete values won’t be able to execute and will instead raise an error. If
|
||||||
|
you want compiled control flow, use structured control flow primitives like
|
||||||
|
lax.cond and lax.while. Some indexing features, like slice-based indexing
|
||||||
|
`A[i:i+5]` for argument-dependent `i`, or boolean-based indexing `A[bool_ind]`
|
||||||
|
for argument-dependent `bool_ind`, produce abstract values of unknown shape and
|
||||||
|
are thus unsupported in `jit` functions.
|
||||||
|
|
||||||
|
> TLDR **Do use**
|
||||||
|
>
|
||||||
|
> * Functional programming
|
||||||
|
> * [Many](https://github.com/google/jax/blob/master/jax/numpy/lax_numpy.py) of NumPy’s
|
||||||
|
> functions (help us add more!)
|
||||||
|
> * [Some](https://github.com/google/jax/tree/master/jax/scipy) SciPy functions
|
||||||
|
> * Indexing and slicing of arrays like `x = A[[5, 1, 7], :, 2:4]`
|
||||||
|
> * Explicit array creation from lists like `A = np.array([x, y])`
|
||||||
|
>
|
||||||
|
> **Don’t use**
|
||||||
|
>
|
||||||
|
> * Assignment into arrays like `A[0, 0] = x`
|
||||||
|
> * Implicit casting to arrays like `np.sum([x, y])` (use `np.sum(np.array([x,
|
||||||
|
> y])` instead)
|
||||||
|
> * `A.dot(B)` method syntax for functions of more than one argument (use
|
||||||
|
> `np.dot(A, B)` instead)
|
||||||
|
> * Side-effects like mutation of arguments or mutation of global variables
|
||||||
|
> * The `out` argument of NumPy functions
|
||||||
|
>
|
||||||
|
> **For jit functions, also don’t use**
|
||||||
|
>
|
||||||
|
> * Control flow based on dynamic values `if x > 0: ...`. Control flow based
|
||||||
|
> on shapes is fine: `if x.shape[0] > 2: ...` and `for subarr in array`.
|
||||||
|
> * Slicing `A[i:i+5]` for dynamic index `i` (use `lax.dynamic_slice` instead)
|
||||||
|
> or boolean indexing `A[bool_ind]` for traced values `bool_ind`.
|
||||||
|
|
||||||
|
You should get loud errors if your code violates any of these.
|
||||||
|
|
||||||
|
## Transformations
|
||||||
|
|
||||||
|
JAX is at its core an extensible system for transforming numerical functions.
|
||||||
|
Here are three key transformations for machine learning research.
|
||||||
|
|
||||||
|
### Automatic differentiation with grad
|
||||||
|
|
||||||
|
JAX has roughly the same API as [Autograd](https://github.com/hips/autograd).
|
||||||
|
The most popular function is `grad` for reverse-mode gradients:
|
||||||
|
|
||||||
|
```python
|
||||||
|
from jax import grad
|
||||||
|
import jax.numpy as np
|
||||||
|
|
||||||
|
def tanh(x): # Define a function
|
||||||
|
y = np.exp(-2.0 * x)
|
||||||
|
return (1.0 - y) / (1.0 + y)
|
||||||
|
|
||||||
|
grad_tanh = grad(tanh) # Obtain its gradient function
|
||||||
|
print(grad_tanh(1.0)) # Evaluate it at x = 1.0
|
||||||
|
# prints 0.41997434161402603
|
||||||
|
```
|
||||||
|
|
||||||
|
You can differentiate to any order with `grad`.
|
||||||
|
|
||||||
|
For more advanced autodiff, you can use `jax.vjp` for reverse-mode
|
||||||
|
vector-Jacobian products and `jax.jvp` for forward-mode Jacobian-vector
|
||||||
|
products. The two can be composed arbitrarily with one another, and with other
|
||||||
|
JAX transformations. Here's one way to compose
|
||||||
|
those to make a function that efficiently computes full Hessian matrices:
|
||||||
|
|
||||||
|
```python
|
||||||
|
from jax import jit, jacfwd, jacrev
|
||||||
|
def hessian(fun):
|
||||||
|
return jit(jacfwd(jacrev(fun)))
|
||||||
|
```
|
||||||
|
|
||||||
|
As with Autograd, you're free to use differentiation with Python control
|
||||||
|
structures:
|
||||||
|
|
||||||
|
```python
|
||||||
|
def abs_val(x):
|
||||||
|
if x > 0:
|
||||||
|
return x
|
||||||
|
else:
|
||||||
|
return -x
|
||||||
|
|
||||||
|
abs_val_grad = grad(abs_val)
|
||||||
|
print(abs_val_grad)(1.0) # prints 1.0
|
||||||
|
print(abs_val_grad)(-1.0) # prints -1.0 (abs_val is re-evaluated)
|
||||||
|
```
|
||||||
|
|
||||||
|
### Compilation with jit
|
||||||
|
|
||||||
|
You can use XLA to compile your functions end-to-end with `jit`, used either as
|
||||||
|
an `@jit` decorator or as a higher-order function.
|
||||||
|
|
||||||
|
```python
|
||||||
|
import jax.numpy as np
|
||||||
|
from jax import jit
|
||||||
|
|
||||||
|
def slow_f(x):
|
||||||
|
# Element-wise ops see a large benefit from fusion
|
||||||
|
return x * x + x * 2.0
|
||||||
|
|
||||||
|
x = np.ones((5000, 5000))
|
||||||
|
fast_f = jit(slow_f)
|
||||||
|
%timeit -n10 -r3 fast_f(x) # ~ 4.5 ms / loop on Titan X
|
||||||
|
%timeit -n10 -r3 slow_f(x) # ~ 14.5 ms / loop (also on GPU via JAX)
|
||||||
|
```
|
||||||
|
|
||||||
|
You can mix `jit` and `grad` and any other JAX transformation however you like.
|
||||||
|
|
||||||
|
### Auto-vectorization with vmap
|
||||||
|
|
||||||
|
JAX enables more program transformations than just forward- and reverse-mode
|
||||||
|
differentiation and compilation. Another example is `vmap`, the vectorizing map.
|
||||||
|
It has the familiar semantics of mapping a function along array axes, but
|
||||||
|
instead of keeping the loop on the outside, it pushes the loop down into a
|
||||||
|
function’s primitive operations for better performance.
|
||||||
|
|
||||||
|
Using `vmap` can save you from having to carry around batch dimensions in your
|
||||||
|
code. For example, consider this simple *unbatched* neural network prediction
|
||||||
|
function:
|
||||||
|
|
||||||
|
```python
|
||||||
|
def predict(params, input_vec):
|
||||||
|
assert input_vec.ndim == 1
|
||||||
|
for W, b in params:
|
||||||
|
output_vec = np.dot(W, input_vec) + b # `input_vec` on the right-hand side!
|
||||||
|
input_vec = np.tanh(output_vec)
|
||||||
|
return output_vec
|
||||||
|
```
|
||||||
|
|
||||||
|
We often instead write `np.dot(inputs, W)` to allow for a batch dimension on the
|
||||||
|
left side of `inputs`, but we’ve written this particular prediction function to
|
||||||
|
apply only to single input vectors. If we wanted to apply this function to a
|
||||||
|
batch of inputs at once, semantically we could just write
|
||||||
|
|
||||||
|
```python
|
||||||
|
from functools import partial
|
||||||
|
predictions = np.stack(list(map(partial(predict, params), input_batch)))
|
||||||
|
```
|
||||||
|
|
||||||
|
But pushing one example through the network at a time would be slow! It’s better
|
||||||
|
to vectorize the computation, so that at every layer we’re doing matrix-matrix
|
||||||
|
multiplies rather than matrix-vector multiplies.
|
||||||
|
|
||||||
|
The `vmap` function does that transformation for us. That is, if we write
|
||||||
|
|
||||||
|
```python
|
||||||
|
from jax import vmap
|
||||||
|
predictions = vmap(partial(predict, params), input_batch)
|
||||||
|
```
|
||||||
|
|
||||||
|
then the `vmap` function will push the outer loop inside the function, and our
|
||||||
|
machine will end up executing matrix-matrix multiplications exactly as if we’d
|
||||||
|
done the batching by hand.
|
||||||
|
|
||||||
|
It’s easy enough to manually batch a simple neural network without `vmap`, but
|
||||||
|
in other cases manual vectorization can be impractical or impossible. Take the
|
||||||
|
problem of efficiently computing per-example gradients: that is, for a fixed set
|
||||||
|
of parameters, we want to compute the gradient of our loss function evaluated
|
||||||
|
separately at each example in a batch. With `vmap`, it’s easy:
|
||||||
|
|
||||||
|
```python
|
||||||
|
per_example_gradients = vmap(partial(grad(loss), params), inputs, targets)
|
||||||
|
```
|
||||||
|
|
||||||
|
Of course, `vmap` can be arbitrarily composed with `jit`, `grad`, and any other
|
||||||
|
JAX transformation! We use `vmap` with both forward- and reverse-mode automatic
|
||||||
|
differentiation for fast Jacobian and Hessian matrix calculations in
|
||||||
|
`jax.jacfwd`, `jax.jacrev`, and `jax.hessian`.
|
||||||
|
|
||||||
|
|
||||||
|
## Random numbers are different
|
||||||
|
|
||||||
|
JAX needs a pseudo-random number generator (PRNG) system to provide
|
||||||
|
reproducible results invariant to compilation boundaries and backends, while
|
||||||
|
also maximizing performance by enabling vectorized generation and
|
||||||
|
parallelization across random calls. The `numpy.random` library doesn’t have
|
||||||
|
those properties. The `jax.random` library meets those needs: it’s functionally
|
||||||
|
pure, but it doesn’t require you to pass stateful random objects back out of
|
||||||
|
every function.
|
||||||
|
|
||||||
|
The `jax.random` library uses
|
||||||
|
[count-based PRNGs](http://www.thesalmons.org/john/random123/papers/random123sc11.pdf)
|
||||||
|
and a functional array-oriented
|
||||||
|
[splitting model](http://publications.lib.chalmers.se/records/fulltext/183348/local_183348.pdf).
|
||||||
|
To generate random values, you call a function like `jax.random.normal` and give
|
||||||
|
it a PRNG key:
|
||||||
|
|
||||||
|
```python
|
||||||
|
import jax.random as random
|
||||||
|
|
||||||
|
key = random.PRNGKey(0)
|
||||||
|
print(random.normal(key, shape=(3,))) # [ 1.81608593 -0.48262325 0.33988902]
|
||||||
|
```
|
||||||
|
|
||||||
|
If we make the same call again with the same key, we get the same values:
|
||||||
|
|
||||||
|
```python
|
||||||
|
print(random.normal(key, shape=(3,))) # [ 1.81608593 -0.48262325 0.33988902]
|
||||||
|
```
|
||||||
|
|
||||||
|
The key never gets updated. So how do we get fresh random values? We use
|
||||||
|
`jax.random.split` to create new keys from existing ones. A common pattern is to
|
||||||
|
split off a new key for every function call that needs random values:
|
||||||
|
|
||||||
|
```python
|
||||||
|
key = random.PRNGKey(0)
|
||||||
|
|
||||||
|
key, subkey = random.split(key)
|
||||||
|
print(random.normal(subkey, shape=(3,))) # [ 1.1378783 -1.22095478 -0.59153646]
|
||||||
|
|
||||||
|
key, subkey = random.split(key)
|
||||||
|
print(random.normal(subkey, shape=(3,))) # [-0.06607265 0.16676566 1.17800343]
|
||||||
|
```
|
||||||
|
|
||||||
|
By splitting the PRNG key, not only do we avoid having to thread random states
|
||||||
|
back out of every function call, but also we can generate multiple random arrays
|
||||||
|
in parallel because we can avoid unnecessary sequential dependencies.
|
||||||
|
|
||||||
|
## Mini-libraries
|
||||||
|
|
||||||
|
JAX provides some small, experimental libraries for machine learning. These
|
||||||
|
libraries are in part about providing tools and in part about serving as
|
||||||
|
examples for how to build such libraries using JAX. Each one is only a few
|
||||||
|
hundred lines of code, so take a look inside and adapt them as you need!
|
||||||
|
|
||||||
|
### Neural-net building with Stax
|
||||||
|
|
||||||
|
**Stax** is a functional neural network building library. The basic idea is that
|
||||||
|
a single layer or an entire network can be modeled as an `(init_fun, apply_fun)`
|
||||||
|
pair. The `init_fun` is used to initialize network parameters and the
|
||||||
|
`apply_fun` takes parameters and inputs to produce outputs. There are
|
||||||
|
constructor functions for common basic pairs, like `Conv` and `Relu`, and these
|
||||||
|
pairs can be composed in serial using `stax.serial` or in parallel using
|
||||||
|
`stax.parallel`.
|
||||||
|
|
||||||
|
Here’s an example:
|
||||||
|
|
||||||
|
```python
|
||||||
|
from jax.experimental import stax
|
||||||
|
from jax.experimental.stax import Conv
|
||||||
|
from jax.experimental.stax import Dense
|
||||||
|
from jax.experimental.stax import MaxPool
|
||||||
|
from jax.experimental.stax import Relu
|
||||||
|
from jax.experimental.stax import LogSoftmax
|
||||||
|
|
||||||
|
# Set up network initialization and evaluation functions
|
||||||
|
net_init, net_apply = stax.serial(
|
||||||
|
Conv(32, (3, 3), padding='SAME'), Relu,
|
||||||
|
Conv(64, (3, 3), padding='SAME'), Relu
|
||||||
|
MaxPool((2, 2)), Flatten,
|
||||||
|
Dense(128), Relu,
|
||||||
|
Dense(10), SoftMax,
|
||||||
|
)
|
||||||
|
|
||||||
|
# Initialize parameters, not committing to a batch shape
|
||||||
|
in_shape = (-1, 28 * 28)
|
||||||
|
out_shape, net_params = net_init(in_shape)
|
||||||
|
|
||||||
|
# Apply network
|
||||||
|
predictions = net_apply(net_params, inputs)
|
||||||
|
```
|
||||||
|
|
||||||
|
### First-order optimization with Minmax
|
||||||
|
|
||||||
|
**Minmax** is an optimization library focused on stochastic first-order
|
||||||
|
optimizers. Every optimizer is modeled as an `(init_fun, update_fun)` pair. The
|
||||||
|
`init_fun` is used to initialize the optimizer state, which could include things
|
||||||
|
like momentum variables, and the `update_fun` accepts a gradient and an
|
||||||
|
optimizer state to produce a new optimizer state. The parameters being optimized
|
||||||
|
can be ndarrays or arbitrarily-nested list/tuple/dict structures, so you can
|
||||||
|
store your parameters however you’d like.
|
||||||
|
|
||||||
|
Here’s an example, using `jit` to compile the whole update end-to-end:
|
||||||
|
|
||||||
|
```python
|
||||||
|
from jax.experimental import minmax
|
||||||
|
from jax import jit
|
||||||
|
|
||||||
|
# Set up an optimizer
|
||||||
|
opt_init, opt_update = minmax.momentum(step_size=1e-3, mass=0.9)
|
||||||
|
|
||||||
|
# Define a compiled update step
|
||||||
|
@jit
|
||||||
|
def step(i, opt_state, batch):
|
||||||
|
params = minmax.get_params(opt_state)
|
||||||
|
g = grad(loss)(params, batch)
|
||||||
|
return opt_update(i, g, opt_state)
|
||||||
|
|
||||||
|
# Optimize parameters in a loop
|
||||||
|
opt_state = opt_init(net_params)
|
||||||
|
for i in range(num_steps):
|
||||||
|
opt_state = step(i, opt_state, next(data_generator))
|
||||||
|
net_params = minmax.get_params(opt_state)
|
||||||
|
```
|
||||||
|
|
||||||
|
## How it works
|
||||||
|
|
||||||
|
Programming in machine learning is about expressing and transforming functions.
|
||||||
|
Transformations include automatic differentiation, compilation for accelerators,
|
||||||
|
and even automatic batching. High-level languages like Python are great for
|
||||||
|
expressing functions, but usually all we can do with them is apply them. We lose
|
||||||
|
access to their internal structure which would let us perform transformations.
|
||||||
|
|
||||||
|
JAX is a tool for specializing and translating high-level Python+NumPy functions
|
||||||
|
into a representation that can be transformed and then lifted back into a Python
|
||||||
|
function.
|
||||||
|
|
||||||
|
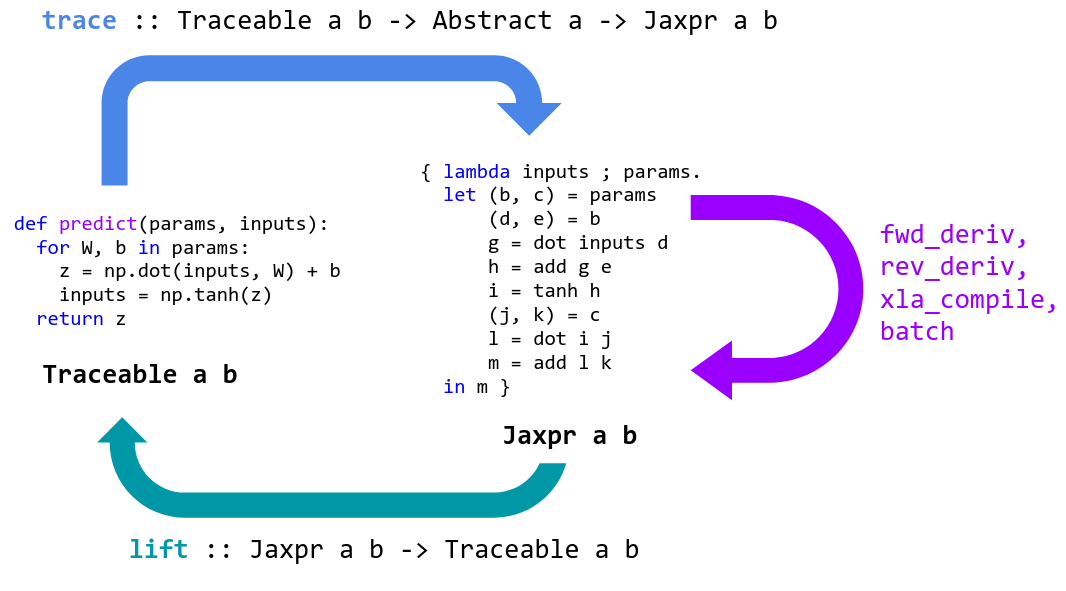
|
||||||
|
|
||||||
|
JAX specializes Python functions by tracing. Tracing a function means monitoring
|
||||||
|
all the basic operations that are applied to its input to produce its output,
|
||||||
|
and recording these operations and the data-flow between them in a directed
|
||||||
|
acyclic graph (DAG). To perform tracing, JAX wraps primitive operations, like
|
||||||
|
basic numerical kernels, so that when they’re called they add themselves to a
|
||||||
|
list of operations performed along with their inputs and outputs. To keep track
|
||||||
|
of how data flows between these primitives, values being tracked are wrapped in
|
||||||
|
instances of the `Tracer` class.
|
||||||
|
|
||||||
|
When a Python function is provided to `grad` or `jit`, it’s wrapped for tracing
|
||||||
|
and returned. When the wrapped function is called, we abstract the concrete
|
||||||
|
arguments provided into instances of the `AbstractValue` class, box them for
|
||||||
|
tracing in instances of the `Tracer` class, and call the function on them.
|
||||||
|
Abstract arguments represent sets of possible values rather than specific
|
||||||
|
values: for example, `jit` abstracts ndarray arguments to abstract values that
|
||||||
|
represent all ndarrays with the same shape and dtype. In contrast, `grad`
|
||||||
|
abstracts ndarray arguments to represent a small neighborhood of the underlying
|
||||||
|
value. By tracing the Python function on these abstract values, we ensure that
|
||||||
|
it’s specialized enough so that it’s tractable to transform, and that it’s still
|
||||||
|
general enough so that the transformed result is useful. These transformed
|
||||||
|
functions are then lifted back into Python callables in a way that allows them
|
||||||
|
to be traced and transformed again as needed.
|
||||||
|
|
||||||
|
The primitive functions that JAX traces are mostly in 1:1 correspondence with
|
||||||
|
[XLA HLO](https://www.tensorflow.org/xla/operation_semantics) and are defined
|
||||||
|
in [lax.py](https://github.com/google/jax/blob/master/jax/lax.py). This 1:1
|
||||||
|
correspondence makes most of the translations to XLA essentially trivial, and
|
||||||
|
ensures we only have a small set of primitives to cover for other
|
||||||
|
transformations like automatic differentiation. The [`jax.numpy`
|
||||||
|
layer](https://github.com/google/jax/blob/master/jax/numpy/) is written in pure
|
||||||
|
Python simply by expressing NumPy functions in terms of the LAX functions (and
|
||||||
|
other NumPy functions we’ve already written). That makes `jax.numpy` easy to
|
||||||
|
extend.
|
||||||
|
|
||||||
|
When you use `jax.numpy`, the underlying LAX primitives are `jit`-compiled
|
||||||
|
behind the scenes, allowing you to write unrestricted Python+Numpy code while
|
||||||
|
still executing each primitive operation on an accelerator.
|
||||||
|
|
||||||
|
But JAX can do more: instead of just compiling and dispatching to a fixed set of
|
||||||
|
individual primitives, you can use `jit` on larger and larger functions to be
|
||||||
|
end-to-end compiled and optimized. For example, instead of just compiling and
|
||||||
|
dispatching a convolution op, you can compile a whole network, or a whole
|
||||||
|
gradient evaluation and optimizer update step.
|
||||||
|
|
||||||
|
The tradeoff is that `jit` functions have to satisfy some additional
|
||||||
|
specialization requirements: since we want to compile traces that are
|
||||||
|
specialized on shapes and dtypes, but not specialized all the way to concrete
|
||||||
|
values, the Python code under a `jit` decorator must be applicable to abstract
|
||||||
|
values. If we try to evaluate `x > 0` on an abstract `x`, the result is an
|
||||||
|
abstract value representing the set `{True, False}`, and so a Python branch like
|
||||||
|
`if x > 0` will raise an error: it doesn’t know which way to go!
|
||||||
|
See [What’s supported](#whats-supported) for more
|
||||||
|
information about `jit` requirements.
|
||||||
|
|
||||||
|
The good news about this tradeoff is that `jit` is opt-in: JAX libraries use
|
||||||
|
`jit` on individual operations and functions behind the scenes, allowing you to
|
||||||
|
write unrestricted Python+Numpy and still make use of a hardware accelerator.
|
||||||
|
But when you want to maximize performance, you can often use `jit` in your own
|
||||||
|
code to compile and end-to-end optimize much bigger functions.
|
||||||
|
|
||||||
|
## What we're working on
|
||||||
|
1. Documentation!
|
||||||
|
2. Cloud TPU support
|
||||||
|
3. Multi-GPU and multi-TPU support
|
||||||
|
4. Full NumPy coverage and some SciPy coverage
|
||||||
|
5. Full coverage for vmap
|
||||||
|
6. Make everything faster
|
||||||
|
* Lowering the XLA function dispatch overhead
|
||||||
|
* Linear algebra routines (MKL on CPU, MAGMA on GPU)
|
||||||
|
7. `cond` and `while` primitives with efficient automatic differentiation
|
||||||
|
|
||||||
|
## Current gotchas
|
||||||
|
|
||||||
|
Some things we don't handle that might surprise NumPy users:
|
||||||
|
1. No in-place mutation syntax. Functional code. Can use lax.dynamic\_update\_slice.
|
||||||
|
2. PRNG can be awkward, and linearity is not checked with a warning.
|
||||||
|
|
||||||
|
## Contributors
|
||||||
|
|
||||||
|
So far, JAX includes lots of help and contributions from [Peter
|
||||||
|
Hawkins](https://github.com/hawkinsp), [Alex
|
||||||
|
Wiltschko](http://github.com/alexbw), George Dahl, [Eli
|
||||||
|
Bendersky](https://github.com/eliben), Zak Stone, [Alexey
|
||||||
|
Radul](https://github.com/axch), Michael Isard, Skye Wanderman-Milne, and many
|
||||||
|
others.
|
||||||
|
|||||||
Loading…
x
Reference in New Issue
Block a user